Продолжаю серию постиков о построении графиков в C++ Builder. Для тех, кто не в курсе, в эту серию уже вошли такие записи:
- Построение косинусов (cos);
- Построение синусов (sin);
- Построение тангенсов (tg);
- Построение котангенсов (ctg).
В общем, данная заметка посвящена тангенсам (tg), а если точнее: построению функции вида a*tg(x)+k. Константы a и k задаются в начале выполнения программы.
Кроме того, в начале выполнения программы должны задаваться минимальное (Xmin) и максимальное (Xmax) значения x, а также шаг, с которым данное значение будет изменяться (dX).
Собственно говоря, разлиновку под график оставим «старой» (рассмотрена в предыдущих статьях, а если точнее – в построении графика косинуса).
Важным моментом является отсутствие функции получения тангенса (tg) в C++ Builder’е. Для этих целей используется выражение, тождественное данной функции. А именно tg(x)=sin(x)/cos(x).
Непосредственно построение графика в можно выполнить C++ Builder так:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | // делаем рисунок видимым Image1->Visible=true; // рассчитываем максимальное и минимальное // значение по оси Y for (X=Xmin;X<=Xmax;X+=dX) { if (cos(X)==0) X+=dX; Y=a*sin(X)/cos(X)+k; if(Ymax<Y) Ymax=Y; if(Ymin>Y) Ymin=Y; } // рассчет масштаба по оси Y if((Ymax-Ymin)==0) MasY=LY-40; else MasY=(LY-40)/(Ymax-Ymin); float B[11]; //вывод промежуточных значений по шкале Y for (i=0;i<=10;i++) { B[i]=50+LY/11*i; AnsiString S = FloatToStrF(Ymax-((Ymax-Ymin)/10)*i,ffFixed,5,2); Image1->Canvas->TextOutA(20,B[i]-15,S); } // как известно, на 0 делить нельзя, а в случае, если косинус // от X равен 0, переходим к следующему шагу if (cos(Xmin)==0) Image1->Canvas->MoveTo(50,LY-(Ymin*(-1)+a*sin(Xmin+dX)/cos(Xmin+dX))*MasY); else Image1->Canvas->MoveTo(50,LY-(Ymin*(-1)+a*sin(Xmin)/cos(Xmin))*MasY); // непосредственное построение графика на канве Image1 for (X=Xmin;X<=Xmax;X+=dX) { Y=a*sin(X)/cos(X)+k; PY=LY-(Ymin*(-1)+Y)*MasY; PX=X*MasX+50; Image1->Canvas->LineTo(PX-Xmin*MasX,PY); } |
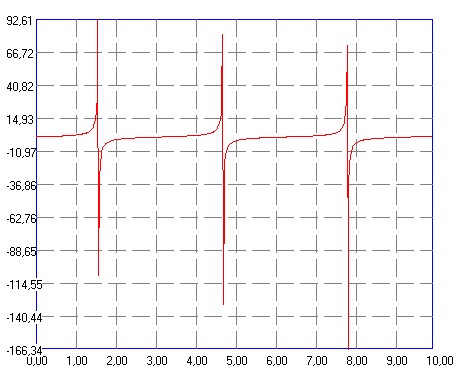
Вот и все. На рисунке график функции тангенс (tg) построенный с такими исходными данными:
1 2 3 4 5 | Xmin=0; Xmax=10; dX=0.02; a=1; k=0; |
Результат. Как известно, функция тангенсов не существует в некоторых точках (там, где синус (находящийся в знаменателе) равен 0). Прерывания я делать не стала (для учебных целей, как по мне, это излишество. Может есть желание переубедить?..
Надеюсь, у вас все получится.
Очень интересно и познавательно, по крайней мере для меня, так как я учитель математики и мне часто надо строить графики тригонометрических функций, спасибо!
)))
Вы, как учитель математики, знаете об этом гораздо больше меня =)
Тангенс с помощью Брезенхема каким образом сделать?
гхм… не знаю =)
Нет идей как закрасить те квадраты, через которые проходят линии?)
Просто закрасить? — Циклически, в зависимости от значения тангенса. Но вам ведь не это нужно, по сути. Нужно разобрать, как строиться алгоритм поточечно…
Мне желательно с помощью алгоритма Брезенхема, но ведь смещение и будет происходить с помощью цикла, верно?
Да, смещение при помощи цикла. Дело не в этом. Алгоритм предполагает, что вы само значение тангенса найдете циклически (не при помощи функции тангенса). А потом, я так понимаю, отразите на графике точки, которые использовались при расчете. Чисто нарисовать проще наоборот — отталкиваясь от рассчитанных значений тангенса.
Если я верно поняла, конечно %)